Rectangle Rotation
Description
A rectangle with sides equal to even integers a and b is drawn on the Cartesian plane. Its center (the intersection point of its diagonals) coincides with the point (0, 0), but the sides of the rectangle are not parallel to the axes; instead, they are forming 45 degree angles with the axes.
How many points with integer coordinates are located inside the given rectangle (including on its sides)?
Example
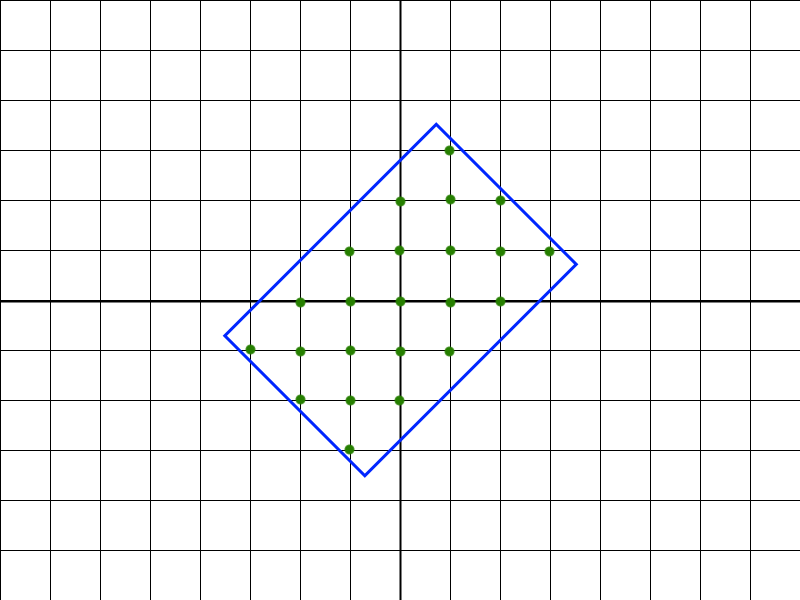
For a = 6 and b = 4, the output should be
rectangleRotation(a, b) = 23.
The following picture illustrates the example, and the 23 points are marked green.
Input/Output
-
[execution time limit] 4 seconds (js)
-
[input] integer a
A positive even integer.
Guaranteed constraints:
2 ≤ a ≤ 50. -
[input] integer b
A positive even integer.
Guaranteed constraints:
2 ≤ b ≤ 50. -
[output] integer
- The number of inner points with integer coordinates.
[JavaScript (ES6)] Syntax Tips
1
2
3
4
5
6
// Prints help message to the console
// Returns a string
function helloWorld(name) {
console.log("This prints to the console when you Run Tests");
return "Hello, " + name;
}
Solution
1
2
3
4
5
6
7
function rectangleRotation(a, b) {
var ld = (a / Math.sqrt(2)) / 2;
var sd = (b / Math.sqrt(2)) / 2;
var rectExt = [2 * Math.floor(ld) + 1, 2 * Math.floor(sd) + 1]
var rectInt = [2 * Math.floor(ld) + (ld % 1 < 0.5 ? 0 : 2), 2 * Math.floor(sd) + (sd % 1 < 0.5 ? 0 : 2)]
return rectExt[0] * rectExt[1] + rectInt[0] * rectInt[1]
}