Codefights

A way to improve your programming skills.

View on GitHub

Count Black Cells

Description

Imagine a white rectangular grid of n rows and m columns divided into two parts by a diagonal line running from the upper left to the lower right corner. Now let’s paint the grid in two colors according to the following rules:

  • A cell is painted black if it has at least one point in common with the diagonal;
  • Otherwise, a cell is painted white.

Count the number of cells painted black.

Example

  • For n = 3 and m = 4, the output should be countBlackCells(n, m) = 6.

    There are 6 cells that have at least one common point with the diagonal and therefore are painted black.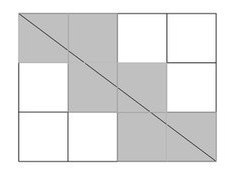

  • For n = 3 and m = 3, the output should be countBlackCells(n, m) = 7.

    7 cells have at least one common point with the diagonal and are painted black.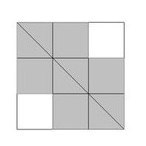

Input/Output

  • [execution time limit] 4 seconds (js)

  • [input] integer n

    The number of rows.

    Guaranteed constraints:
    1 \leq n \leq 10^5.

  • [input] integer m

    The number of columns.

    Guaranteed constraints:
    1 \leq m \leq 10^5.

  • [output] integer

    • The number of black cells.

[JavaScript (ES6)] Syntax Tips

1
2
3
4
5
6

// Prints help message to the console
// Returns a string
function helloWorld(name) {
console.log("This prints to the console when you Run Tests");
return "Hello, " + name;
}

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

function countBlackCells(n, m) {
  var s;
  if (n > m) {
    s = n;
    n = m;
    m = s;
  }
  s = 0;
  var r = 0;
  var t = 0;
  for (var i = 0; i < n / gcd(m, n); i++) {
    t = m / n + r;
    s += Math.ceil(t);
    r = (t - 0.000001) % 1;
  }
  function gcd(a, b) {
    if (!b) {
      return a;
    }
    return gcd(b, a % b);
  }
  return gcd(m, n) * s + (gcd(m, n) - 1) * 2;
}